
On solving this, we will get the equation as:
The relation among the relativistic energy, momentum, and the rest mass of the electron after the collision is:įrom eq (5) in (6): (p0 - p1)² + 2km = p² ….(7)įrom eq (5) in (6): (p0 - p1)² + 2km = p0² + p1² - 2p0p1 cosΘ
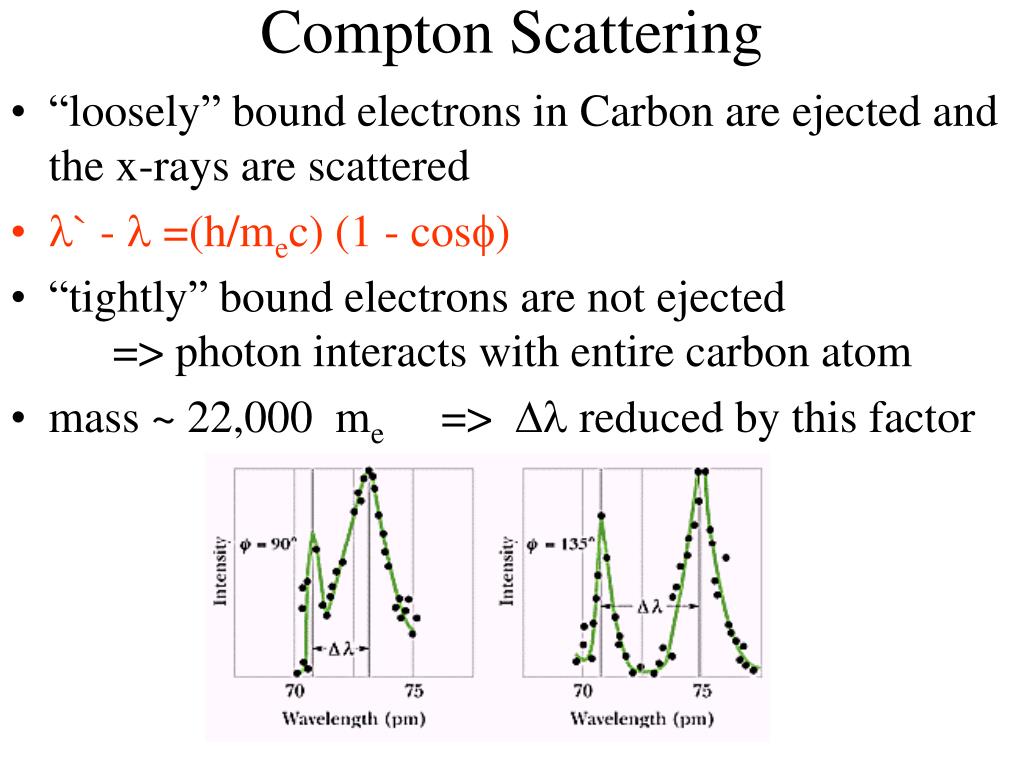
#Relation between theta and phi in compton effect Pc#
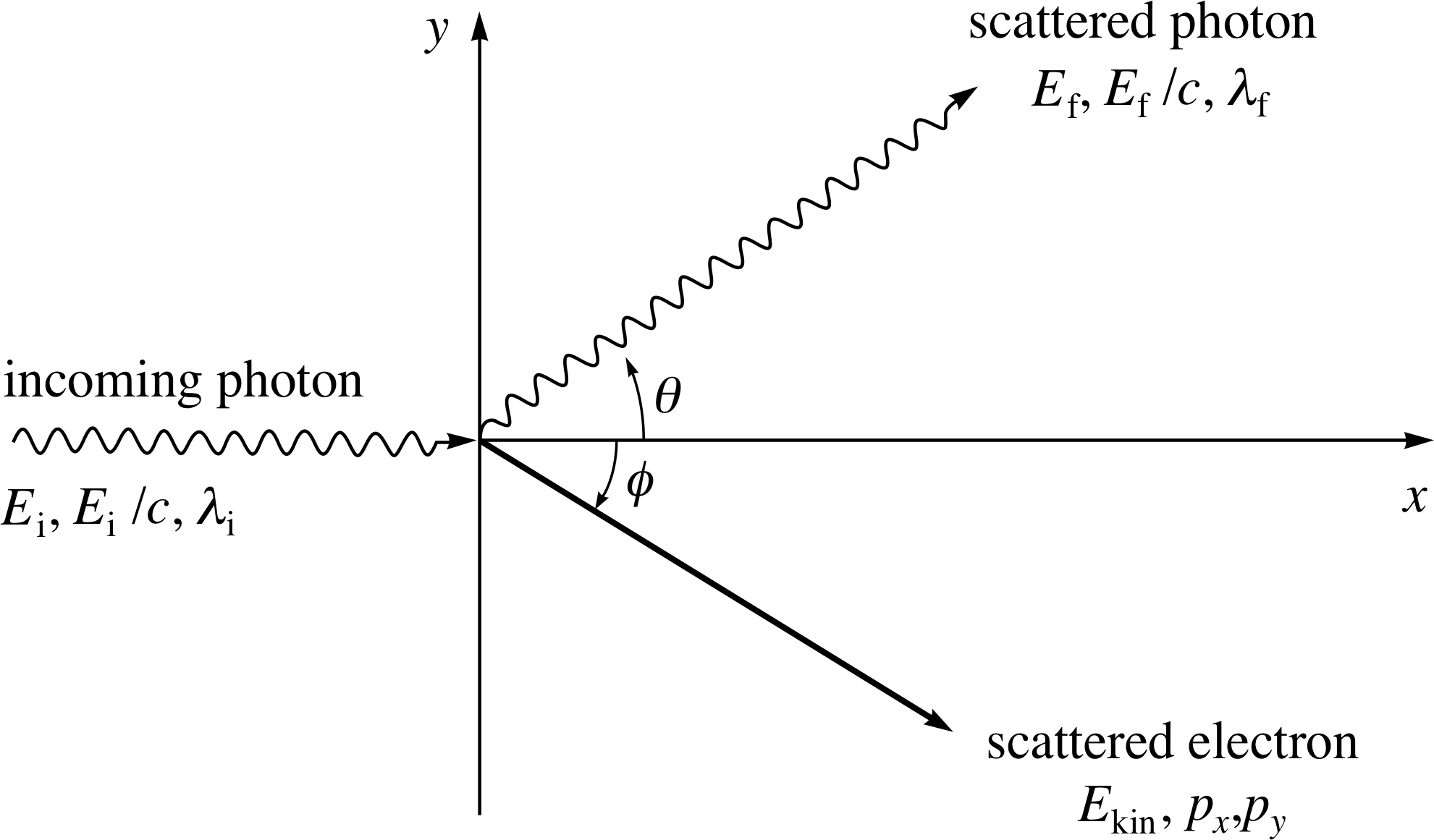
So, we represent the energy of a photon as E = pc The momentum of a photon is given by: p = h/λ = hf/λf = E/c po 2+ p1 2 cosΘ + 2p0 p1cosΘ + p1sin 2Θ = p 2Cos 2Ф + p 2Sin 2ФĪpplying the law of conservation of energy:.And, adding equations (3) and (4), we get:.Now, squaring equations (1) & (2), we get: Applying the law of conservation of momentum along the X-axis and Y axis we get, The momentum remains conserved at all axis. The angle formed by the scattering photon with the x-axis is Θ.Īn electron, on the other hand, gains momentum ‘p’ and kinetic energy ‘k’ to form an angle with the x-axis, Ф.When the photon collides with an electron along the x-axis, the kinetic energy decreases to E1’ and momentum to p1’.Initially, the momentum and kinetic energy of the photon is p0’ and E0’.Let us take a photon that collides with an electron.


 0 kommentar(er)
0 kommentar(er)
